Sensitivities in SEIR models: a (very) quick investigation
The COVID-19 pandemic recently caused and still causes major problems in several respects. Also, (mathematical) modelers face difficulties in simulating and predicting the final size of the pandemic.
The dynamics of the pandemic are often simulated by compartmental models. Although they are known to contain some uncertainties, they can be utilized to reliably demonstrate the effect of intervention strategies.
Goal
The goal of this post is to show that a particular compartmental model, the SEIR model, is not useful for prediction purposes due to high sensitivities in its model parameters, which is of interest since some of the more sophisticated models are based on SEIR. For example, the COVID-19 model of the German Robert Koch-Institut (RKI) is an adjusted SEIR model with more compartments to reflect the complexity of the COVID-19 pandemic; see their publication.
We assume that the reader is already familiar with the SEIR model and some statistics. A short description can be seen on Wikipedia.
Remark. This post is not a scientific statement. It only/superficially describes the result of a (very) quick investigation of SEIR parameter sensitivities that the author conducted in his spare time.
SEIR model
As a reminder, SEIR (excluding births and deaths) describes the dynamics of an infectious disease with the ODE system \begin{align} \frac{dS}{dt} &= -\beta S \frac{I}{N}, \newline \frac{dE}{dt} &= \beta S \frac{I}{N} - \alpha E, \newline \frac{dI}{dt} &= \alpha E - \gamma I, \newline \frac{dR}{dt} &= \gamma I. \end{align}
It models four compartments (susceptibles – S, exposed – E, infectious – I, removed – R) and the transitions between them involving model parameters for transition rates.
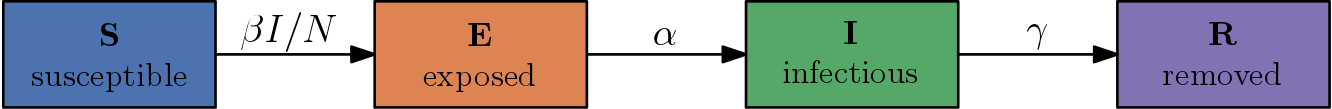
The initial conditions for the ODE system above are \begin{align} S(0) &= N-I(0), \newline E(0) &= 0, \newline I(0) &= I_0, \newline R(0) &= 0, \end{align} where \(N\) is the (fixed) total number of individuals. Note that \begin{equation} S(t)+E(t)+I(t)+R(t)=N\end{equation} for all \(t\geq0\).
Remark. The unit of time \(t\) is weeks.
The model parameters are:
- \(\beta\) – transmission rate (average number of contacts per person per time),
- \(\alpha\) – latency rate, or equivalently, \(\alpha^{-1}\) – mean duration of the latency period,
- \(\gamma\) – recovery rate, or equivalently, \(\gamma^{-1}\) – mean duration of the infection,
- \(I_0\) – initial number of infections.
One important characteristic of an infection is the so-called basic reproduction number denoted by \(\mathcal{R}_0\). It indicates the expected number of direct infections caused by exactly one case in a population where all other individuals are susceptible. For the SEIR model, it can be computed to \begin{equation}\mathcal{R}_0=\frac{\beta}{\gamma}.\end{equation}
RKI’s assumptions
In their publication, RKI makes the following assumptions:
- \(\mathcal{R}_0=2\),
- \(\alpha^{-1}=3/7\),
- \(\gamma^{-1}=9/7\),
- \(I_0=1000\).
It follows that \(\beta = 14/9\).
Sensitivity study
In the following, we additionally assume a total population size of \(N=80 \cdot 10^6 = 80\text{ million}\).
We set \begin{equation}\theta = (\beta, \alpha, \gamma, I_0)^\top \in \mathbf{R}^4\end{equation} as the parameter vector and regard it as a random vector following a uniform distribution \(\mu=\mathcal{U}(R)\) on a rectangle \(R\) such that \begin{equation}\theta_i \in [\theta_i^-,\theta_i^+]\end{equation} for all \(i=1,\ldots,4\). The boundaries of the rectangle are determined by a perturbation of \(\pm p\%\) of the RKI parameters above. For example, \begin{equation} \beta^{\pm} = 14/9 \cdot \left(1 \pm \frac{p}{100}\right). \end{equation}
Let us set the simulation time to \(T=60\text{ [weeks]}\) and define two maps. The map \begin{equation} \mathcal{G}_1(\theta) := (I(t))_{t=0,1,\ldots,T} \end{equation} takes a particular parameter \(\theta\) and computes the corresponding number of infectious individuals for times \(t=0,1,\ldots,T\). Additionally, the map \begin{equation} \mathcal{G}_2(\theta) := \mathop{\mathrm{arg\,max}}_{t=0,1,\ldots,T}{I(t)} \end{equation} computes the peak time of the infectious compartment.
For a fixed \(p\in[0,100]\), we investigate two corresponding distributions, \(\mu(\mathcal{G}_1^{-1}(\cdot))\) and \(\mu(\mathcal{G}_2^{-1}(\cdot))\) by sampling \(M=1000\) times from \(\mu\) and computing \(\mathcal{G}_{1}\) and \(\mathcal{G}_{2}\) for each sample.
For a perturbation of \(p=5\%\), the (approximate) distributions are plotted in the following figure.

On the left, we see the distribution \(\mu(\mathcal{G}_1^{-1}(\cdot))\) with its mean, median, and a 95% quantile band, i.e. the band between the 2.5% and 97.5% quantile. The right plot displays the distribution of the peaks. The corresponding 95% quantile interval here is \([20, 24]\).
The same quantities are plotted for \(p=10\%\) in the following figure.

The 95% quantile interval for the infectious peaks on the right is \([19, 27]\).
Remark. This is not a serious sensitivity analysis. There might be parameters that are more sensitive than others which is not visible by the investigated quantities and plots.
Conclusion
The predictions of SEIR models are subject to uncertainties caused by sensitivities in its parameters.
For example, a perturbation of \(p=10\%\), which is likely to occur in practice, causes an uncertainty in the peak time of infectious individuals of about 8 weeks in the sense of a 95% quantile interval.
Source code
The source code to reproduce the above figures is put in a repository at bitbucket.
Since the samples for the plotted distributions are independent, we computed the corresponding ODE solutions in parallel using a program called launcher.